近日,丘成桐数学科学中心助理教授金龙与Semyon Dyatlov教授合作论文《双曲曲面上半经典测度具有全支集》(Semiclassical measures on hyperbolic surfaces have full support)在国际顶尖数学期刊《Acta Mathematica》(《数学学报》)上在线发表。该论文成果对于理解量子混沌系统具有重要的意义。著名数学家Steven Zelditch教授说,这篇论文是近十年来这方面最好的文章。

曲面或区域上的Laplace算子特征函数是量子态的简单模型,其在半经典极限下的分布情况由半经典测度描述,与对应的经典力学系统的性质有紧密的联系。负曲率曲面上的测地流是经典的混沌系统,刻画其上的半经典测度是量子混沌领域中最重要的一个问题。
Rudnick与Sarnak对此提出量子唯一遍历猜想,认为负曲率曲面上的半经典测度一定是Liouville测度,即特征函数在半经典极限下呈现一致分布。此前对于半经典测度的研究集中在得到熵的下界估计,而金龙与Dyatlov的研究论文利用被称为“分形不确定性原理”的新工具打破了这一局限。他们对于曲率为负常数的双曲曲面研究证明了半经典测度具有全支集,即半经典极限下特征函数不能完全的集中在一个子集上。
由此还可推出双曲曲面上线性Schrödinger方程可由任意非空开集控制。
不同类型区域上高频特征函数的概率密度分布
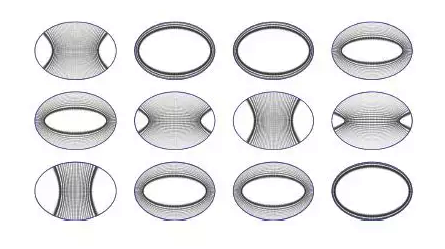
椭圆区域的经典系统是规则的,对应的特征函数集中在部分子集上。

双曲区域上的经典系统是混沌的,对应的特征函数趋于一致分布。

金龙,1988年出生,助理教授。丘成桐数学科学中心由美国普渡大学引进。他本科毕业于北京大学数学系,2015年获美国加州大学伯克利分校博士学位,师从Maciej Zworski教授。随后在美国哈佛大学、普渡大学先后从事博士后研究工作,研究方向主要在与微分方程和数学物理相关的谱理论及散射理论。在该篇论文研究过程中,金龙曾多次访问数学中心。入职中心后,金龙老师除开展研究工作外,将承担分析与偏微分方程学科方向的教学并指导相关专业研究生等工作。
《Acta Mathematica》是公认发表难度最大的数学期刊之一,由瑞典皇家科学院Mittag-Leffler研究所1882年创刊,是全球四大顶级数学期刊之一,涵盖数学各领域最高质量的研究论文,季刊发行,每年2卷,每卷2期,全年共十余篇论文。