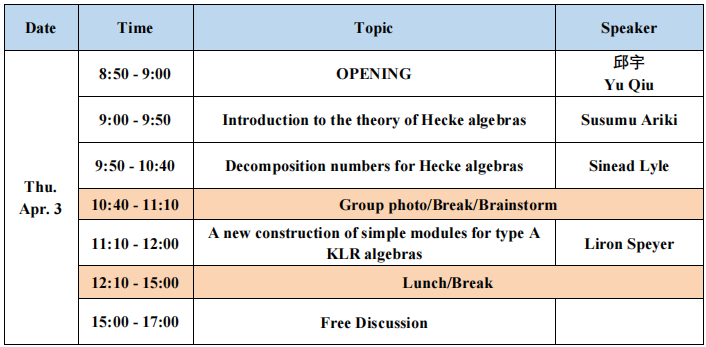
Venue:

8:50 - 12:10, Shuangqing C548

15:00 - 17:00, Shuangqing B534

Schedule:

Title: Introduction to the theory of Hecke algebras
Abstract: I start with explaining how Dipper and James initiated the modular representation theory of Hecke algebras, and the first half of my talk ends with the theory of cyclotomic Hecke algebras. In the second half, I will explain how those early results are absorbed into the theory of cyclotomic quiver Hecke algebras. In the course of the explanation, basic materials such as decomposition numbers, KLR algebra etc. will be explained, which would help the audience prepare for the next two talks.

Title: Decomposition numbers for Hecke algebras
Abstract: An important open problem in the representation theory of the Hecke algebras is to find the composition factors of certain modules which are known as Specht modules. In this talk I will look at some of the methods used to compute these decomposition numbers. I will explain how to partition the Specht modules into blocks and then we will look at some blocks for which the decomposition numbers are known.

Title: A new construction of simple modules for type A KLR algebras
Abstract: Cuspidal systems parameterise KLR algebra representations via root partitions, each associated to a ‘proper standard module’, which has a simple head. These simple heads form a complete set of simple modules. Working in affine type A with an arbitrary convex preorder, we construct these same simple modules as simple heads of skew Specht modules. An advantage of this construction is that it is much more explicit and combinatorial than previous descriptions. In this talk, I will describe this construction, and how it arises from studying RoCK blocks in level 1 (i.e. for type A Hecke algebras). This is based on joint work with Muth, Nicewicz, and Sutton.