地点:双清综合楼C548

标题和摘要(按报告顺序)
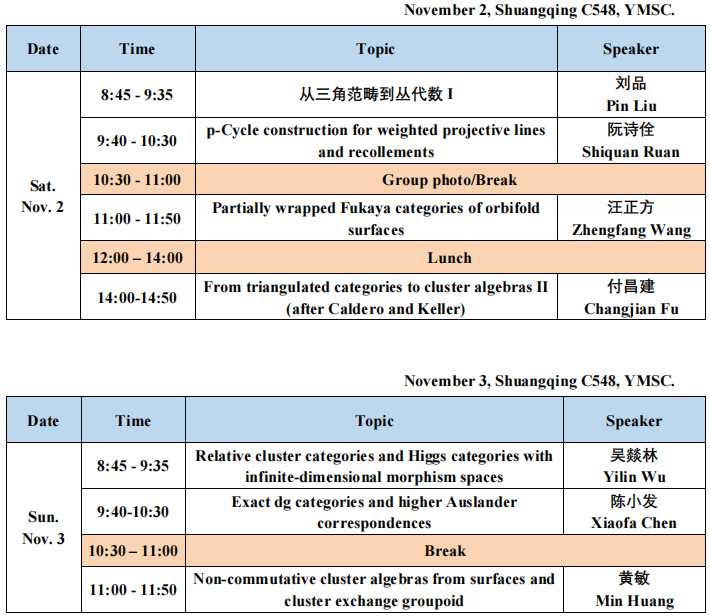
报告人:刘品 西南交通大学
标题:从三角范畴到丛代数I
摘要:本次报告将介绍Caldero-Keller的丛乘法公式,基本复刻了孔伯恩在挪威科技大学做的同名报告。
报告人:阮诗佺 厦门大学
标题:p-Cycle construction for weighted projective lines and recollements
摘要:In this talk, I will show how to construct recollements and ladders for exceptional curves by using reduction/insertion functors due to p-cycle construction. As applications to weighted projective lines, we will classify recollements for the category of coherent sheaves over a weighted projective line, and give an explicit description of ladders in two different levels: the bounded derived category of coherent sheaves and the stable category of vector bundles.
报告人:汪正方 南京大学
标题:Partially wrapped Fukaya categories of orbifold surfaces
摘要:Motivated by the consideration of $A_\infty$-deformations of gentle algebras, we define partially wrapped Fukaya categories of surfaces with orbifold points by giving several equivalent constructions. In particular, this gives rise to geometric realisations of the perfect derived categories of skew-gentle algebras in terms of dissections of the orbifold surfaces into polygons. By considering a wider class of dissections, we are able to identify all dissections giving rise to formal $A_\infity$ algebras and thus a large class of associative algebras derived equivalent to skew-gentle algebras. This is joint work with Severin Barmeier and Sibylle Schroll.
报告人:付昌建 四川大学
标题:From triangulated categories to cluster algebras II (after Caldero and Keller)
摘要:In this talk, I will review one of the foundation of additive categorication of cluster algebras by Caldero and Keller. In particular, we will see how to prove several conjecutures for acyclic cluster algebras by representations of quivers.
报告人:吴燚林 中国科学技术大学
标题:Relative cluster categories and Higgs categories with infinite-dimensional morphism spaces.
摘要:Cluster categories were introduced in 2006 by Buan-Marsh-Reineke-Reiten-Todorov in order to categorify acyclic cluster algebras without coefficients. Their construction was generalized by Amiot to Jacobi-finite quiver with potential (2009). Later, Plamondon generalized it to arbitrary cluster algebras associated with quivers (2009 and 2011). Cluster algebras with coefficients are important since they appear in nature as coordinate algebras of varieties like Grassmannians, double Bruhat cells, unipotent cells,... The work of Geiss-Leclerc-Schröer often yields Frobenius exact categories which allow to categorify such cluster algebras. In previous work, we have constructed Higgs categories and relative cluster categories in the Jacobi-finite setting (arXiv:2109.03707). Higgs categories generalize the Frobenius categories used by Geiss-Leclerc-Schröer.
In this talk, we will present the construction of the Higgs category and of the relative cluster category in the Jacobi-infinite setting. As in the Jacobi-finite case, the Higgs category is no longer exact but still extriangulated in the sense of Nakaoka-Palu (2019). We also give the construction of a cluster character in this setting. This is a report on joint work with Bernhard Keller (arXiv:2307.12279).
报告人:陈小发 中国科学技术大学
标题:Exact dg categories and higher Auslander correspondences
摘要:Exact dg categories allow to enhance extriangulated categories and to perform constructions like functor categories or tensor products for which the extriangulated structure alone does not suffice. In particular, they yield a new approach to and a generalization of higher versions of Auslander correspondences as established by Iyama and by Iyama-Solberg, for example. In this talk, I will give an introduction to exact dg categories and sketch their application to correspondences on the example of 0-Auslander categories. We will see in particular that the framework of exact dg categories allows to enhance the correspondences to equivalences of infinity-groupoids.
报告人:黄敏 中山大学(珠海)
标题: Non-commutative cluster algebras from surfaces and cluster exchange groupoid
摘要: This is a joint work with Arkady Berenstein and Vladimir Retakh. In the talk, I will introduce a class of non-commutative cluster algebras which satisfy non-commutative Laurent phenomenon. We will also introduce non-commutative g-vectors and use them to realize the cluster exchange groupoid introduced by King-Qiu.






