
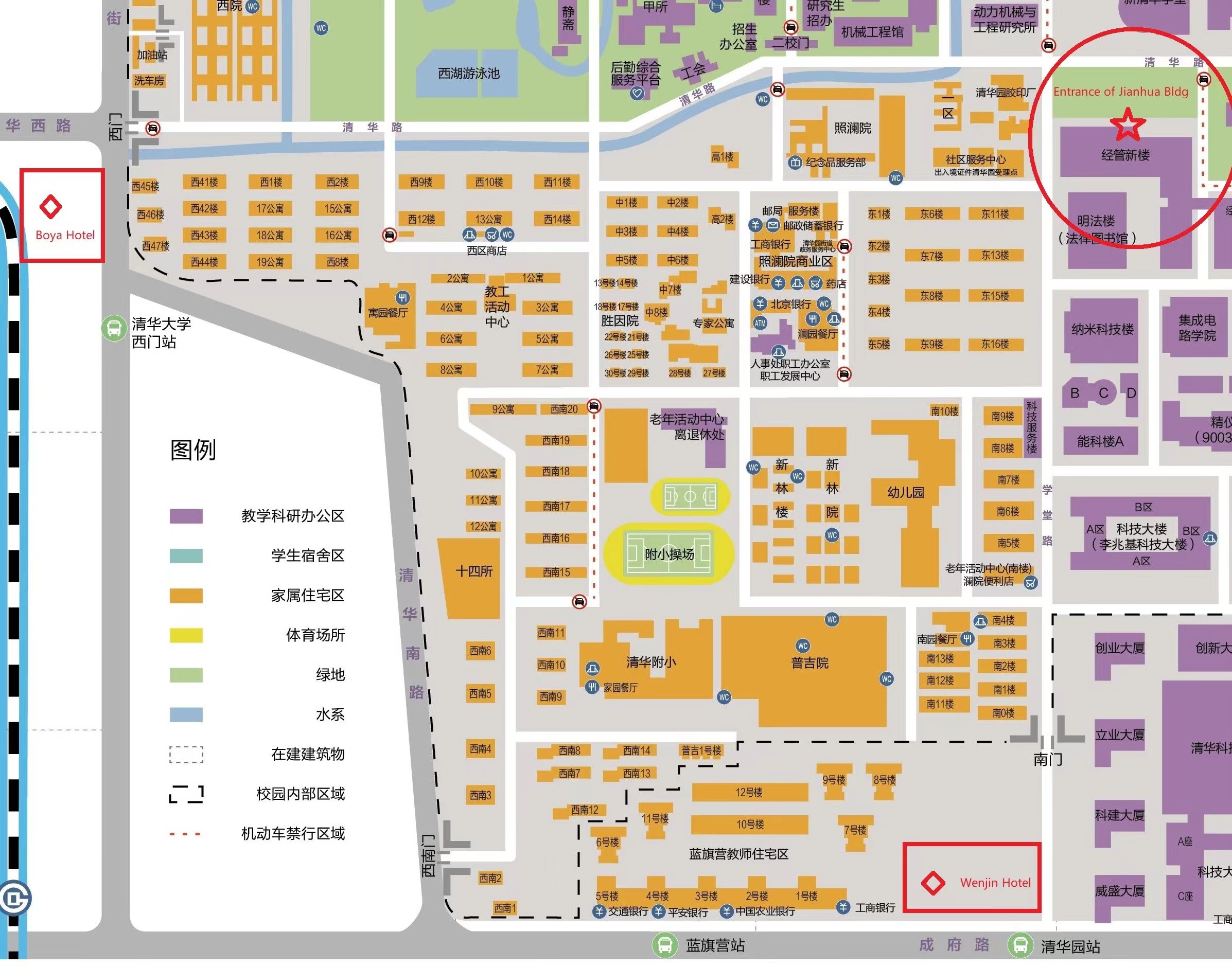
Time & Venue
July 10-14, 2023
LG1-16, Jianhua Building (建华楼), Tsinghua University
Online
Zoom ID: 830 1358 0116
Password: 123456
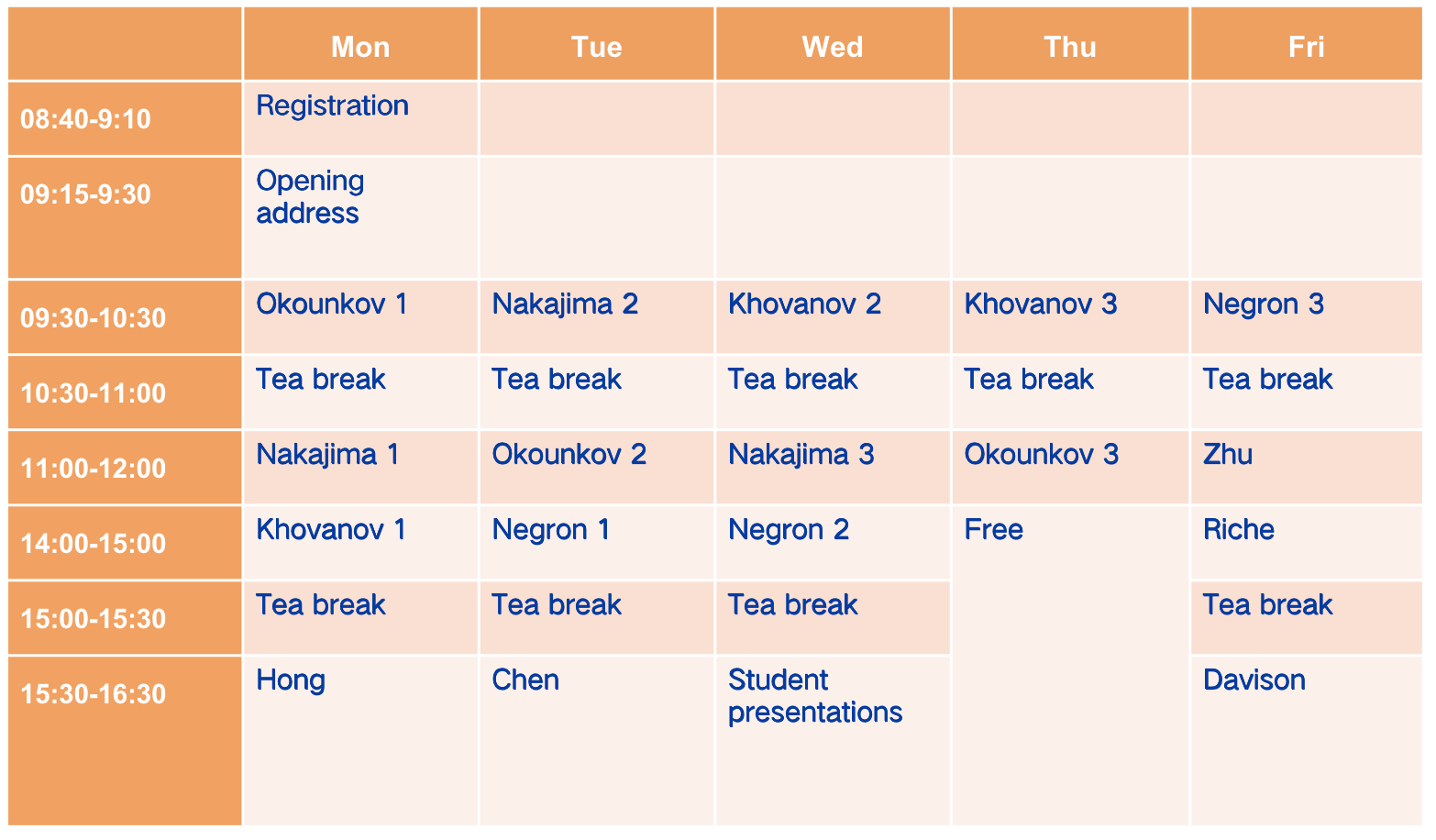
Schedule
Registration Link
https://f.kdocs.cn/g/ZqtSBl5M/
OVERVIEW
Representation theory is the study of the basic symmetries of mathematics and physics. The fundamental aims of geometric representation theory are to uncover the deeper geometric and categorical structures underlying the familiar objects of representation theory and harmonic analysis, and to apply the resulting insights to the resolution of classical problems. The geometric study of representations often reveals deeper layers of structure in the form of categorification. Categorification typically replaces numbers (such as character values) by vector spaces (typically cohomology groups), and vector spaces (such as representation rings) by categories (typically of sheaves).
A primary goal of the workshop is to introduce some of the latest developments and important research topics in this field to graduate students and young scholars.
Organizers
Penghui Li
Nicolai Reshetikhin
Peng Shan
Changjian Su
Speakers
Lin Chen
IAS
Title: Observe LG via Gr_G and collision of disks
Abstract: Given a DG category acted by the loop group LG, one can define a factorization D(Gr_G)-module category, where Gr_G is the Beilinson—Drinfeld affine Grassmannian, viewed as a factorization indscheme. We will show this construction loses no information: it gives a fully faithful 2-functor from LG-mod(DGCat) to Gr_G-mod_fact(DGCat). We will also explain the role of this result in the local Geometric Langlands program. This is a report of the incoming joint work of Dennis Gaitsgory, Yuchen Fu, David Yang and the speaker.
Ben Davison
University of Edinburgh
Title: Kac polynomials and generalised Kac-Moody algebras
Abstract: Given a quiver Q and a dimension vector d, Victor Kac proved in the early '80s that the map sending each prime power q to the number of absolutely indecomposable d-dimensional representations of Q over the field of cardinality q extends to a polynomial with integer coefficients. At the same time he conjectured that the constant terms of this polynomial record the weight multiplicities of the Kac-Moody algebra associated to the underlying graph of Q (assuming for the moment that Q has no loops). This conjecture was proved by Tamas Hausel, using the arithmetic geometry of Nakajima quiver varieties.
In this talk I will explain that in fact all of the coefficients of the Kac polynomials of Q (even allowing loops) record the weight multiplicities of a generalised Kac-Moody (a.k.a. Borcherds) algebra, at least partially answering a question of Andrei Okounkov from 10 years ago. The spaces of Chevalley generators of this GKM algebra are moreover identified with the cohomologically graded pieces of the intersection cohomology of certain singular Nakajima quiver varieties. This is joint work with Lucien Hennecart and Sebastian Schlegel Mejia.
Jiuzu Hong
University of North Carolina at Chapel Hill
Title: A refined coherent property for affine Demazure modules
Abstract:
The coherent conjecture of Pappas-Rapoport (reformulated and proved by Zhu), asserts that the dimension of global sections of line bundles on Schubert varieties in affine Grassmannians, is equal to the dimension of global sections of line bundles on certain union of Schubert varieties in affine flag varieties. This can be translated to the dimension invariance of certain union of Demazure modules (kind of symmetrization over finite Weyl group) in any integrable highest weight module of affine Lie algebra when the level is fixed.
In this talk, I will explain a refined version of such coherent property, i.e. such union of Demazure modules admits the same action of a reductive subalgebra depending upon the affine dominant weight. If time permits, I will also discuss the twisted analogue. This talk will be based on a joint work with Huanhuan Yu (in progress).
Mikhail Khovanov
Columbia University
Title: Universal construction, foams and link homology
Abstract: We will explain the construction of sl(N) link homology theories which categorify the HOMFLYPT link invariant and Reshetikhin-Turaev sl(N) quantum link invariants. Combinatorial-topological construction of these homology theories is based on the theory of foams, which are suitable decorated 2-dimensional CW-complexes in 3-space. A version of foam theory is related to the 4-color theorem and Kronheimer-Mrowka 3-orbiford homology theory. Link homology foam theories will be reviewed in detail, starting with N=3 case.
Hiraku Nakajima
Kavli IPMU
Title: Coulomb branches of orthosymplectic quiver gauge theories
Cris Negron
University of Southern California
Title: Quantum groups and categorical representation theory
Abstract: I will discuss the representation theory of quantum groups at almost-arbitrary roots of unity. Here we mean integrable representations for Lusztig's divided power quantum enveloping algebra for a particular choice of semi-simple G and complex parameter q, specifically. I will focus on relationships between the big quantum group, small quantum group, and a classical dual group. Indeed, we will see how this dual group acts as a bridge between the representation theories of the big quantum group and its small counterpart, and allows one to translate results between these two settings. Examples of such phenomena in geometric representations theory and in logarithmic conformal field theory will be discussed.
Andrei Okounkov
UC Berkeley
Title: Eisenstein series and related topics
Abstract:
This will be an introductory discussion of Eisenstein series as well as spectral and enumerative problems associated with them. My plan is to discuss all phenomena in the minimal interesting generality (split, unramified, etc. and sometimes for just SL(2)).
Simon Riche
Université Clermont Auvergne
Title: Perverse sheaves on affine flag varieties, coherent sheaves on Steinberg varieties, and Harish-Chandra bimodules
Abstract: I will report on a joint work with Roman Bezrukavnikov aiming at constructing a "modular Bezrukavnikov equivalence", i.e. an equivalence of categories relating perverse sheaves on an affine flag variety, with coefficients in a field of positive characteristic, and coherent sheaves on a suitable version of the Steinberg variety, thereby providing a categorical upgrade of the isomorphism between the two standard geometric realizations of the affine Hecke algebra. The link between these two worlds is provided by (modular, affine) Soergel bimodules and Harish-Chandra bimodules. If time permits I will also discuss applications of this construction to modular representations of reductive groups.
Xinwen Zhu
Stanford University
Title: The unipotent categorical local Langlands correspondence
Abstract: I will discuss a conjectural categorical form of the (arithmetic) local Langlands correspondence for p-adic groups and establish the unipotent part of such correspondence (for characteristic zero coefficient field). Joint work with Tamir Hemo.
Student Presentations
Schedule:
15:30-15:45 Quan Situ
15:45-16:00 Tianqing Zhu
16:00-16:15 Dmitry Solovyev
16:15-16:30 Xuanzhong Dai
16:30-16:45 Pengcheng Li
16:45-17:00 Veronica Pasquarella
17:00-17:15 Bingyu Zhang
Title and abstract:
Xuanzhong Dai (RIMS, Kyoto University)
Title: Chiral de Rham complex and modular theories
Abstract: Chiral de Rham complex constructed by Malikov et al. in 1998, is a sheaf of vertex operator algebras on any complex manifold or nonsingular algebraic variety. For any congruence subgroup $\Gamma$, we study the vertex algebra constructed from the $\Gamma$-invariant global sections of the chiral de Rham complex on the upper half plane with certain cuspidal conditions. We exhibit a linear basis of the $\Gamma$-invariant algebra consisting of liftings of modular forms, and compute its character formula. In 1994, D. Zagier, Y. Manin, and W. Eholzer speculated that the Rankin-Cohen brackets of modular forms should be related to a vertex operator algebra. We demonstrate that the vertex operations of $\Gamma$-invariant algebras can be expressed by the Rankin-Cohen brackets.
Pengcheng Li (Tsinghua University)
Title: Categorical actions and derived equivalences for finite odd-dimensional orthogonal groups
Abstract: In this talk, I will give a brief introduction to Kac-Moody categorification and Broue's abelian defect group conjecture. We prove that Broue's abelian defect group conjecture is true for the finite odd-dimensional orthogonal groups SO_{2n+1}(q) at linear primes with q odd. We frist make use of the reduction theorem of Bonnafe-Dat-Rouquier to reduce the problem to isolated blocks. Then we construct a categorical action of a Kac-Moody algebra on the category of quadratic unipotent representations of the various groups SO_{2n+1}(q) in non-defining characteristic, by generalizing the corresponding work of Dudas-Varagnolo-Vasserot for unipotent representations. This is one of the main ingredients of our work which may be of independent interest. To obtain derived equivalences of blocks and their Brauer correspondents, we define and investigate isolated RoCK blocks. Finally, we establish the desired derived equivalence based on the work of Chuang-Rouquier that categorical actions provide derived equivalences between certain weight spaces. This is a joint work with Yanjun Liu and Jiping Zhang.
Veronica Pasquarella (University of Cambridge)
Title: Drinfeld Centers from Magnetic Quivers
Abstract: In this talk I will show that magnetic quivers encode the necessary information for determining the Drinfeld center in the symmetry topological field theory (SymTFT) associated to a given absolute theory. The crucial argument resides in their common aim of generalising homological mirror symmetry. (Based on arXiv:2306.12471).
Quan Situ (Tsinghua University)
Title: Hybrid Quantum Group and its Category O
Abstract: In this talk we introduce the hybrid quantum group, whose category O can be viewed as a quantum analogue of BGG category O. We compute the center of each block, constructing an algebra isomorphism to the cohomology of certain (partial) affine flag variety. We will also discuss categorical interpretation of this result for the Steinberg block and the principal block.
Dmitry Solovyev (Tsinghua University)
Title: The limit shape phenomena in representation theory of quantum groups at roots of unity.
Abstract: We explore statistics of irreducible and indecomposable components in large tensor products of fundamental representation of U_q(sl_2) with divided powers(also known as the big quantum group) with respect to Plancherel and character probability measures. We describe the limit shape and fluctuations in its vicinity for both the Plancherel measure and the character measure.
Bingyu Zhang (University of Southern Denmark)
Title: Categorical trace in microlocal geometry of cotangent bundle
Abstract: We can define a Tamarkin category to all open sets in a cotangent bundle using microlocal theory of sheaves, which is known as a symplectic invariant of the corresponding open set. We will explain some geometric applications of categorical trace of Tamarkin categories, including capacities and a Viterbo isomorphism, and some related conjectures. Part of the talk is based on a joint work with Christopher Kuo and Vivek Shende.
Tianqing Zhu (Tsinghua University)
Title: Quantum difference equation for affine type A quiver varieties.
Abstract: The quantum difference equation (qde) is the $q$-difference equation which is proposed by Okounkov and Smirnov to encode the $K$-theoretic twisted quasimap counting for the Nakajima quiver varieties. In this talk, we will give a direct quantum toroidal algebra $U_{q,t}(\hat{\hat{\mf{sl}}}_{n})$ construction for the qde of the affine type $A$ quiver varieties, and we will give the explicit formula for the quantum difference equation. We will give the example of the Hilbert scheme $\text{Hilb}_{n}(\widehat{\mbb{C}^2/\mbb{Z}_{r}})$. And we conjecture that these qde is equivalent to the one given by Okounkov and Smirnov. And if time permits, we will discuss its relation to the quantum differential equation for the affine type $A$ quiver varieties.
Scan QR code to apply
Due to limited space, we may not be able to accept all the registered participants. A notification will be sent to those who will not be admitted. Unfortunately, there will be no financial support.
For the undergraduate or the PhD student outside Tsinghua University, please acquire a recommendation letter from the advisor and submit to the email address:
georepymsc@outlook.com
Deadline for registration: 2023/05/31
Deadline for recommendation letter: 2023/06/15
Videos: http://archive.ymsc.tsinghua.edu.cn/pacm_lecture?html=Workshop_on_Geometric_Representation_Theory_and_Applications.html






