
Schedule
2023-04-22
9:30 - 10:20
Konstantin Khanin (University of Toronto)
Title: On the KPZ problem and statistics of stochastic flows
Abstract: In this talk we will discuss a geometrical approach to the problem of the KPZ Universality. Instead of looking at the height (interface) function and Airy processes, we will focus on the statistics of shocks and points of concentration of mass. We will also discuss the connection with the problem of the coalescing Brownian motions and coalescing fractional Brownian motions.
10:40 - 11:20
Xiangchan Zhu 朱湘禅(Chinese Academy of Sciences)
Title: Stochastic Navier-Stokes equations via convex integration
Abstract: In this talk I will talk about our recent work on the three dimensional stochastic Navier-Stokes equations via convex integration method. First we establish non-uniqueness in law, existence and non-uniqueness of probabilistically strong solutions and non-uniqueness of the associated Markov processes. Second we prove existence of infinitely many stationary solutions as well as ergodic stationary solutions to the stochastic Navier-Stokes and Euler equations. Third we obtain global-in-time existence and non-uniqueness of probabilistically strong solutions to the three dimensional Navier–Stokes system driven by space-time white noise. In this setting, the convective term is ill-defined in the classical sense and probabilistic renormalization is required. Finally I will show the existence, non-uniqueness, non-Guassianity and non-unique ergodicity for singular quasi geostrophic equation in the critical and supercritical regime.
11:20 - 12:00
Timothée Bénard (University of Cambridge)
Title: Limit theorems on nilpotent Lie groups
Abstract: I will talk about my recent work with E. Breuillard establishing limit theorems for random walks on nilpotent Lie groups. Most previous works assumed the law of increment to be centered in the abelianization of the group. Our major contribution is to allow the law of increment to be non-centered. In this case, new phenomena appear: the large scale geometry of the walk depends on the increment average, and the limiting measure in the central limit theorem may not have full support in the group.
14:00 - 14:40
Peisen Li 李培森(Beijing Institute of Technology)
Title: Quasi-stationary distribution for the branching process with competition
Abstract: We consider continuous-state branching process with competition introduced in Berestycki, Fittipaldi and Fontbona (Probab. Theory Relat. Fields, 2018). We establish the strong Feller property and irreducibility. These properties allow us to obtain a sufficient condition for the uniqueness and existence of the quasi-stationary distribution for the process. This is a joint work with Jian Wang and Xiaowen Zhou.
14:40 - 15:20
Zhenyao Sun 孙振尧(Beijing Institute of Technology)
Title: On the regularisation of reaction-diffusion equations by the Wight-Fisher white noise
Abstract: We give the weak uniqueness of a class of one-dimensional stochastic reaction-diffusion equations with Wright-Fisher white noise. Our results cover examples such as
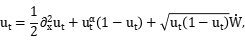
where 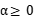 and
and 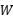 is a space-time white noise. Traditionally, the weak uniqueness of this example is only established when the drift is Lipschitz, i.e.,
is a space-time white noise. Traditionally, the weak uniqueness of this example is only established when the drift is Lipschitz, i.e., 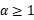 . However, recent work (Comm. Math. Phys. 384 (2021), no. 2) has shown that this weak uniqueness also holds when
. However, recent work (Comm. Math. Phys. 384 (2021), no. 2) has shown that this weak uniqueness also holds when 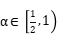 , provided the initial value
, provided the initial value 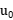 has a compact interface. Our results imply the weak uniqueness of the aforementioned example for every
has a compact interface. Our results imply the weak uniqueness of the aforementioned example for every 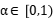 without any assumptions regarding the support of the initial value. This is based on ongoing joint work with Clayton Barnes and Leonid Mytnik.
without any assumptions regarding the support of the initial value. This is based on ongoing joint work with Clayton Barnes and Leonid Mytnik.
16:00 - 16:30
Ziyu Liu 刘子愉(Peking University)
Title: Eventual continuity approach to verifying unique ergodicity of SPDEs
Abstract: We formulate a new criterion of the asymptotic stability for some non-equicontinuous Markov semigroups, the so-called eventually continuous semigroups. In particular, we provide a non-equicontinuous Markov semigroup example with essential randomness, which is asymptotically stable. We further apply the eventual continuity approach to the study of the ergodicity of stochastic partial differential equations with multiplicative noise. We apply the generalized coupling method to verify the eventual continuity and combine it with the uniform irreducibility to verify the unique ergodicity.
16:30 - 17:00
Houqi Su 苏厚奇(Chinese Academy of Sciences)
Title: Stability of rarefaction for stochastic viscous conservation law
Abstract: It was proved in our previews work that the rarefaction wave for the stochastic Burgers equation with transport noise is time-asymptotically. This talk is concerned with more general flux, viscosity and conservative noise. By manipulating the weakly monotone methods, we firstly prove the global well-possedness of strong solutions for general  initial data. Furthermore, we show that the rarefaction wave is still time-asymptotically stable for general stochastic viscous conservation laws with
initial data. Furthermore, we show that the rarefaction wave is still time-asymptotically stable for general stochastic viscous conservation laws with 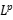 time-decay rates. Finally, the
time-decay rates. Finally, the 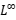 convergence rates towards the rarefaction waves are also obtained if the initial data is small. The main ingredient contains
convergence rates towards the rarefaction waves are also obtained if the initial data is small. The main ingredient contains 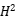 regularity of strong solution. This is a joint work with Zhao Dong and Feimin Huang.
regularity of strong solution. This is a joint work with Zhao Dong and Feimin Huang.
2023-04-23
9:30 - 10:20
Tadahisa Funaki (BIMSA)
Title: Motion by mean curvature from nongradient Glauber-Kawasaki dynamics
Abstract: We first give an introduction to the problem of the hydrodynamic limit. Then, we present the derivation of the motion by mean curvature from Glauber-Kawasaki dynamics of nongradient type. This extends a series of our recent results obtained under gradient condition to general nongradient case.
10:40 - 11:20
Fei Pu 蒲飞(Beijing Normal University)
Title: Hitting with probability one for stochastic heat equations with additive noise
Abstract: I will present some results on the hitting probabilities for the solution to systems of stochastic heat equations. In particular, we consider a system of 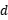 stochastic heat equations with additive noise subject to Dirichlet boundary conditions. We show that for any bounded Borel set with positive
stochastic heat equations with additive noise subject to Dirichlet boundary conditions. We show that for any bounded Borel set with positive 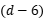 -dimensional capacity, the solution visits this set almost surely. This is based on joint work with Robert C. Dalang.
-dimensional capacity, the solution visits this set almost surely. This is based on joint work with Robert C. Dalang.
11:20 - 12:00
Scott Smith (Chinese Academy of Sciences)
Title: The Master Loop Equation for Lattice Yang Mills
Abstract: I will give an introduction to the master loop equation and explain how to derive it in a simple way from the corresponding Langevin dynamic. Based on joint work with Hao Shen and Rongchan Zhu.





